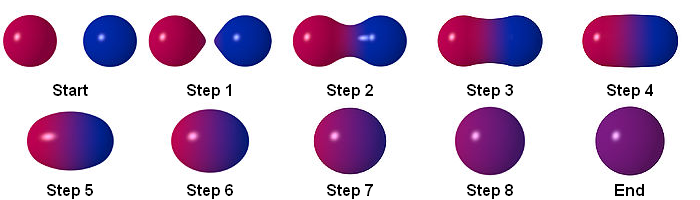
- Before we start
- IDEs and plugins used
- Definition
- Defining circles
- Marching squares method
- Project structure
- Screenshots
This project is based on following articles:
- "Metaballs and Marching Squares" by Jamie Wong
- "Marching Squares Implementation" by Tom Gibara
- "Polygonising a scalar field" by Paul Bourke
- "Metaballs" from Wikipedia
Special thanks to @aptem336 for helping me to seek for information and implementations of similar projects. Go check his own implementation of 3D metaballs.
The application is developed as the part of the project for computer graphics course at Irkutsk National Research Techincal University.
Metaballs are organic-looking objects that can be defined as a function in n-dimensions. - Wikipedia
Metaballs from Wikipedia
I'm gonna show you the way to code 2D metaballs and explain some math-related stuff.
Based on Jamie Wong article [1]
As we have two dimensional metaballs the problem is to find all the points inside a circle limited by its bounds. Let’s look at equation defining a circle with center at (x0,y0) and radius r:
If we want to model all the points inside circle including its bound:
Having all the interacting circles we can model all the points inside them if a circle of i is defined with center at (xi,yi) and radius ri:
And finally we get the equation defining two dimensional metaballs:
Code:
public static double f(double[] B) {
double sum = 0;
for (Circle circle : Data.Balls) {
// SUM (r_i)^2 / ((x - x_i)^2 + (y - y_i)^2)
sum += Math.pow(Data.circleSize, 2) / ((Math.pow(B[0] - circle.x, 2) + Math.pow(B[1] - circle.y, 2)));
}
return sum;
}Marching squares is a computer graphics algorithm that generates contours for a two-dimensional scalar field (rectangular array of individual numerical values) - Wikipedia
Best solution with detailed explanation is given in Paul Bourke article [3].
All kinds of grid cell angles
Binary tables:
/**
* Binary tables
*/
static int[] edgeTable = {
0x0, 0x9, 0x3, 0xA,
0x6, 0xF, 0x5, 0xC,
0xC, 0x5, 0xF, 0x6,
0xA, 0x3, 0x9, 0x0
};
static int[][] lineTable = {
{-1, -1, -1, -1},
{3, 0, -1, -1, -1, -1},
{0, 1, -1, -1, -1, -1},
{1, 3, -1, -1, -1, -1},
{1, 2, -1, -1, -1, -1},
{1, 2, 3, 0, -1, -1},
{0, 2, -1, -1, -1, -1},
{2, 3, -1, -1, -1, -1},
{2, 3, -1, -1, -1, -1},
{0, 2, -1, -1, -1, -1},
{0, 1, 2, 3, -1, -1},
{1, 2, -1, -1, -1, -1},
{1, 3, -1, -1, -1, -1},
{0, 1, -1, -1, -1, -1},
{3, 0, -1, -1, -1, -1},
{-1, -1, -1, -1, -1, -1}
};Marching squares method:
private static void buildSquare(int i, int j) {
double[][] gridP = wMath.gridPoints(i, j);
double[] gridV = wMath.gridValues(i, j);
int squareIndex = wMath.squareIndex(gridV);
int edges = wMath.edgeTable[squareIndex];
if (edges != 0) {
double[][] vertList = new double[4][2];
if ((edges & 1) > 0) {
vertList[0] = wMath.vertexInter(gridP[0], gridP[1], gridV[0], gridV[1]);
}
if ((edges & 2) > 0) {
vertList[1] = wMath.vertexInter(gridP[1], gridP[2], gridV[1], gridV[2]);
}
if ((edges & 4) > 0) {
vertList[2] = wMath.vertexInter(gridP[2], gridP[3], gridV[2], gridV[3]);
}
if ((edges & 8) > 0) {
vertList[3] = wMath.vertexInter(gridP[3], gridP[0], gridV[3], gridV[0]);
}
double[][][] lines = new double[2][2][2];
int nlines = 0;
for (i = 0; wMath.lineTable[squareIndex][i] != -1; i += 2) {
lines[nlines][0] = vertList[wMath.lineTable[squareIndex][i]];
lines[nlines][1] = vertList[wMath.lineTable[squareIndex][i + 1]];
nlines++;
}
for (j = 0; j < nlines; j++) {
Grid.createLine(lines[j], Data.metaColor);
}
}
}Linear interpolation:
public static double[] vertexInter(double[] D, double[] B, double fD, double fB) {
double[] mS = new double[]{(D[0] + B[0]) / 2, (D[1] + B[1]) / 2};
double[] Q = new double[2];
if (Math.abs(1 - fD) < 0.0005) {
return D;
} else if (Math.abs(1 - fB) < 0.0005) {
return B;
} else if (Math.abs(fD - fB) < 0.0005) {
return mS;
} else {
double exp = (1 - fB) / (fD - fB);
Q[0] = B[0] + (D[0] - B[0]) * exp;
Q[1] = B[1] + (D[1] - B[1]) * exp;
}
return Q;
}The project is made up of 8 classes:
- Circle class defines metaballs' structure and methods and implements basic physics
- Data class stores fields of parameters for metaballs
- Grid class stands for grid definition
- Impulse class contains a method giving impusle to metaball
- Interface class builds interface
- Listener class is obviously to listen to different program events like keyboard or mouse events
- Metaballs class is the main class of the program
- wMath class defines all the methods calculating all math-related parameters
Main window:
Showing grid inside circles:
Marching squares mode enabled:
With enabled interpolation:
Scaling up a grid: