Lindblad-ME

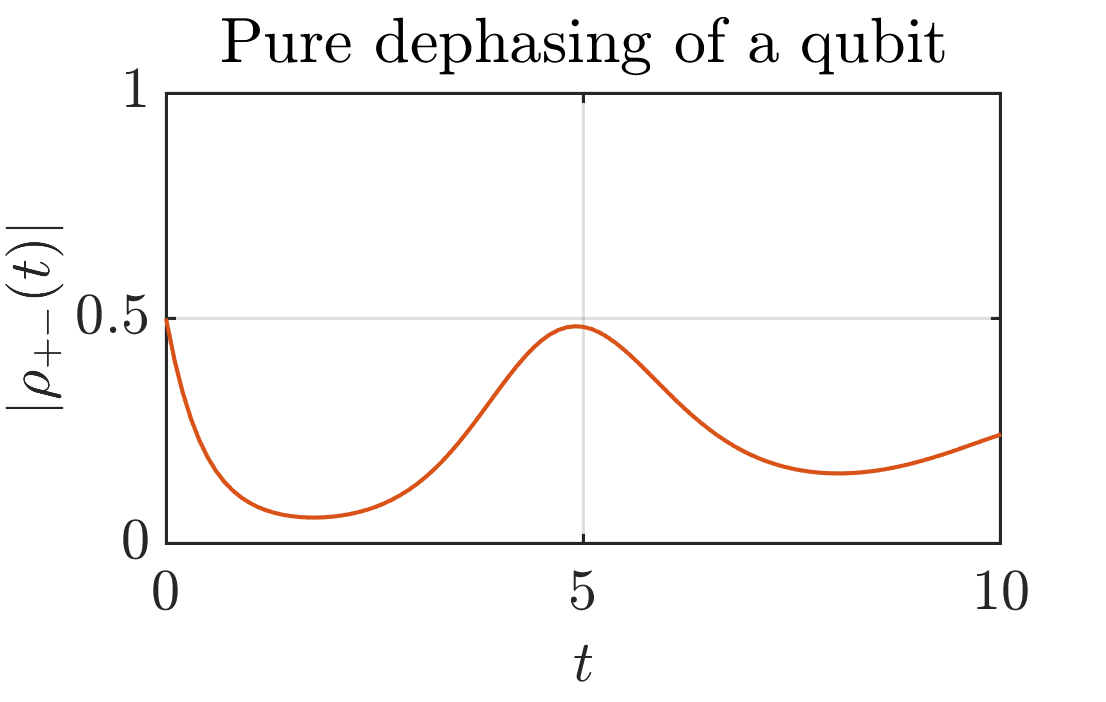
This simple matlab function allows you to compute the density matrix evolution under a Lindblad Master Equation $$\dot{\rho}(t) = \mathcal{L}[\rho] = -i [H(t),\rho(t)] + \sum_k \gamma_k(t)\left( L_k^\dagger \rho (t) L_k -{1\over 2} { L_k^\dagger L_k,\rho(t)}\right)$$

The function requires you to specify the Hamiltonia $H$, Lindblad operators $L_k$ and their corresponding rates $\gamma_k$, and the time interval you want the equation solved. If you use the time depentdent ME you also need to specify the decay rates and the Hamiltonian at this points.

How it works

This function vectorizes the density matrix $|i\rangle \langle j| \to |i,j\rangle$. Then the function computes the linear map $T_{ij} = Tr(F_i^\dagger \mathcal{L} [F_j])$ where the $F_i$ form an orthonormal basis in the space $|i,j\rangle$. This procedure allows to simply write a differential equation $|\dot{\rho}(t)\rangle = T |\rho(t)\rangle$, which is a system of ODEs which is solved with the ODE45 function included in MATLAB.

Examples

Pure dephasing

The Lindblad operator that gives rise to pure dephasing dynamics is given by 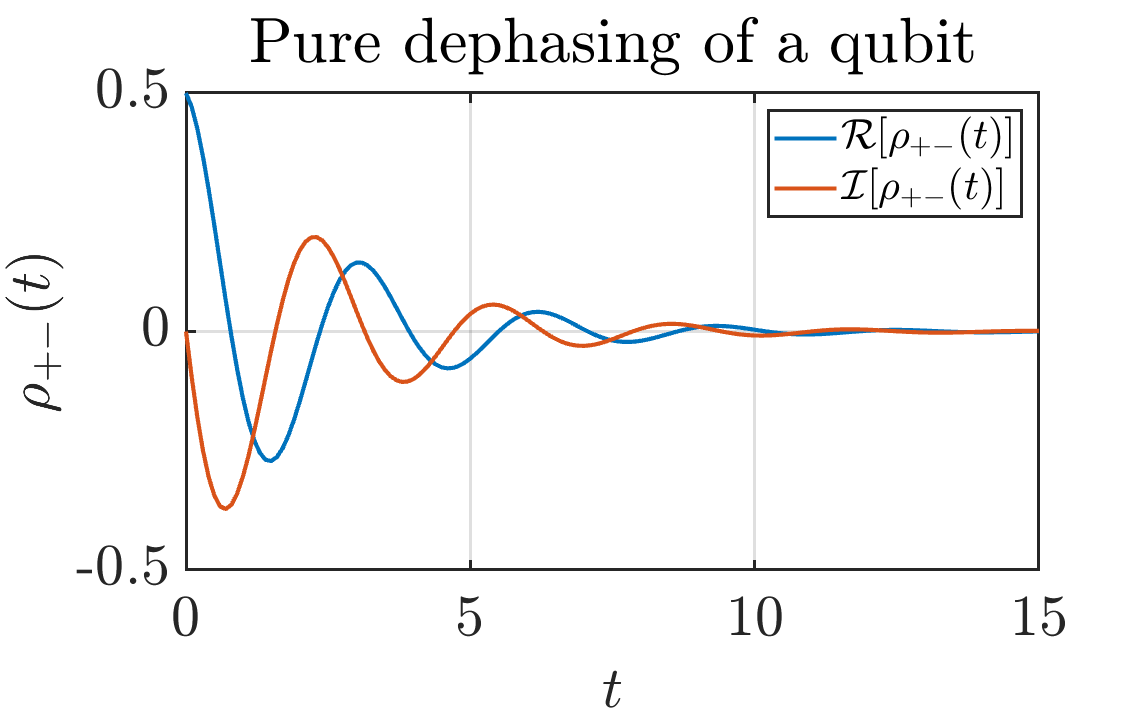$\sigma_z$. Take a look the example file to see an instructive example on how to use the program in this case.

Time dependent pure dephasing

In this case a time dependent Hamiltonian and decay rate is given. The Lindblad operator is still $\sigma_z$ giving rise to pure dephasing. In this case the decay rate becomes negative at some intervals where the coherence experience revivals.