#The Fast Bilateral Solver
The Bilater Solver is a novel algorithm for edge-aware smoothing that combines the flexibility and speed of simple filtering approaches with the accuracy of domain-specific optimization algorithms. This algorithm was presented by Jonathan T. Barron and Ben Poole as an ECCV2016 oral and best paper nominee. Algorithm details and applications can be found in https://arxiv.org/pdf/1511.03296.pdf . (This moudle will be contributed to OpenCV_contrib soon)
[TOC]
##Introduce
###Algorithm
- We begin by presenting the objective and optimization techniques that make up our bilateral solver. Let us assume that we have some per-pixel input quantities t (the “target” value, see Figure 1a) and some per-pixel confidence of those quantities c (Figure 1c), both represented as vectorized images. Let us also assume that we have some “reference” image (Figure 1d), which is a normal RGB image. Our goal is to recover an “output” vector x (Figure 1b), which will resemble the input target where the confidence is large while being smooth and tightly aligned to edges in the reference image. We will accomplish this by constructing an optimization problem consisting of an image-dependent smoothness term that encourages x to be bilateral-smooth, and a data-fidelity term that minimizes the squared residual between x and the target t weighted by our confidence c: $$minimize\frac{\lambda}{2}\sum_{i,j}\widehat{W}{i,j}(x_i-x_j)^{2}+\sum{i}(c_i-t_i)^{2} \quad (1)$$
- The smoothness term in this optimization problem is built around an affinity matrix Ŵ , which is a bistochastized version of a bilateral affinity matrix W . Each element of the bilateral affinity matrix
$W_{i,j}$ reflects the affinity between pixels i and j in the reference image in the YUV colorspace:$$W_{i,j} = \exp(-\frac{\left |[p_i^x,p_i^y]-[[p_j^x,p_j^y]]\right |}{2\sigma_{xy}^2}-\frac{(p_i^l-p_j^l)^2}{2\sigma_{l}^2}-\frac{\left |[p_i^u,p_i^v]-[[p_j^u,p_j^v]]\right |}{2\sigma_{uv}^2})\quad (2)$$ - Where
$p_i$ is a pixel in our reference image with a spatial position$(p_i^x, p_i^y )$ and color$(p_i^l , p_i^u , p_i^v )$ . The$\sigma_{xy} , \sigma_l$ , and$σ_{uv}$ parameters control the extent of the spatial, luma, and chroma support of the filter, respectively. - This W matrix is commonly used in the bilateral filter, an edge-preserving filter that blurs within regions but not across edges by locally adapting the filter to the image content. There are techniques for speeding up bilateral filtering which treat the filter as a “splat/blur/slice” procedure: pixel values are “splatted” onto a small set of vertices in a grid or lattice (a soft histogramming operation), then those vertex values are blurred, and then the filtered pixel values are produced via a “slice” (an interpolation) of the blurred vertex values. These splat/blur/slice filtering approaches all correspond to a compact and efficient factorization of W :
$$W = S^T\overline{B}S\quad (3)$$ - Barron et al. built on this idea to allow for optimization problems to be “splatted” and solved in bilateral-space. They use a “simplified” bilateral grid and a technique for producing bistochastization matrices
$D_n , D_m$ that together give the the following equivalences:$$\widehat{W} = S^TD_m^{-1}D_n\overline{B}D_nD_m^{-1}S , SS^T = D_m\quad (4)$$ - They also perform a variable substitution, which reformulates a high-dimensional pixel-space optimization problem in terms of the lower-dimensional bilateral-space vertices:
$$x = S^Ty\quad (5)$$ - Where y is a small vector of values for each bilateral-space vertex, while x is a large vector of values for each pixel. With these tools we can not only reformulate our pixel-space loss function in Eq 1 in bilateral-space, but we can rewrite that bilateral-space loss function in a quadratic form:
$$minimize\frac{1}{2}y^TAy - b^Ty + c\quad (6)$$ $$A = \lambda(D_m - D_n\overline{B}D_n) + diag(S\textbf c)$$ $$b = S(\textbf c \circ \textbf t)$$ $$c = \frac{1}{2}(\textbf c \circ \textbf t)^T\textbf t$$ - Where
$\circ$ is the Hadamard product. A derivation of this reformulation can be found in the supplement. While the optimization problem in Equation 1 is intractably expensive to solve naively, in this bilateral-space formulation optimization can be performed quickly. Minimizing that quadratic form is equivalent to solving a sparse linear system:$$Ay = b\quad (7)$$ - We can produce a pixel-space solution x̂ by simply slicing the solution to that linear system:
$$\widehat{x} = S^T(A^{-1}b) \quad (8)$$ - With this we can describe our algorithm, which we will refer to as the “bilateral solver.” The input to the solver is a reference RGB image, a target image that contains noisy observed quantities which we wish to improve, and a confidence image. We construct a simplified bilateral grid from the reference image, which is bistochastized as in [2] (see the supplement for details), and with that we construct the A matrix and b vector described in Equation 6 which are used to solve the linear system in Equation 8 to produce an output image. If we have multiple target images (with the same reference and confidence images) then we can construct a larger linear system in which b has many columns, and solve for each channel simultaneously using the same A matrix. In this many-target case, if b is low rank then that property can be exploited to accelerate optimization, as we show in the supplement.
###Implementation
- Splat+Blur+Slice Procedure
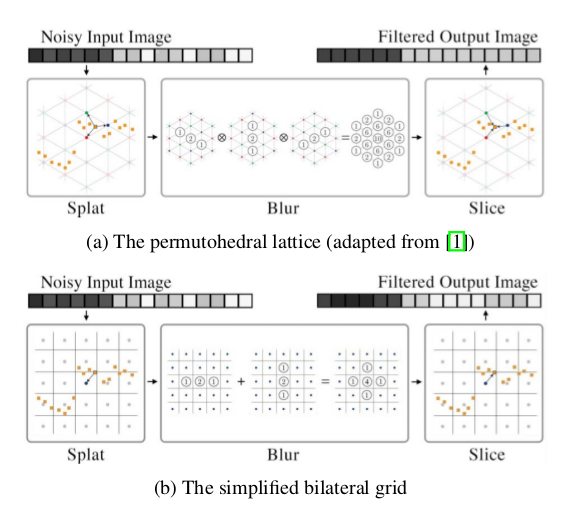The two bilateral representations used in the paper, here shown filtering a toy one-dimensional grayscale image of a step-edge. This toy image corresponds to a 2D space visualized here (x = pixel location, y = pixel value) while in the paper we use RGB images, which corresponds to a 5D space (XYRGB). The lattice (Fig 2a) uses barycen-tric interpolation to map pixels to vertices and requires d+1 blurring operations, where d is the dimensionality of the space. The simplified bilateral grid (Fig 2b) uses nearest-neighbor interpolation and requires d blurring operations which are summed rather than done in sequence. The grid is cheaper to construct and to use than the lattice, but the use of hard assignments means that the filtered output often has blocky piecewise-constant artifacts.
Slice:
void FastBilateralSolverFilterImpl::Splat(Eigen::VectorXf& input, Eigen::VectorXf& output)
{
output.setZero();
for (int i = 0; i < int(splat_idx.size()); i++)
{
output(splat_idx[i]) += input(i);
}
}
Blur:
void FastBilateralSolverFilterImpl::Blur(Eigen::VectorXf& input, Eigen::VectorXf& output)
{
output.setZero();
output = input * 10;
for (int i = 0; i < int(blur_idx.size()); i++)
{
output(blur_idx[i].first) += input(blur_idx[i].second);
}
}
Slice:
void FastBilateralSolverFilterImpl::Slice(Eigen::VectorXf& input, Eigen::VectorXf& output)
{
output.setZero();
for (int i = 0; i < int(splat_idx.size()); i++)
{
output(i) = input(splat_idx[i]);
}
}
- Conjugate Gradient
In this moudle, the Eigen ConjugateGradient moudle is uesd for solving the Ay = b
// solve Ay = b
Eigen::ConjugateGradient<Eigen::SparseMatrix<float>, Eigen::Lower|Eigen::Upper> cg;
cg.compute(A);
cg.setMaxIterations(bs_param.cg_maxiter);
cg.setTolerance(bs_param.cg_tol);
// y = cg.solve(b);
y = cg.solveWithGuess(b,y0);
std::cout << "#iterations: " << cg.iterations() << std::endl;
std::cout << "estimated error: " << cg.error() << std::endl;
- Diagrammatize
st=>start: Start
e=>end
inr=>operation: Imput reference image
int=>operation: Imput target image
bg=>operation: construct BilateralGrid
sl=>operation: construct SliceMatrix
bl=>operation: construct BlurMatrix
A1=>operation: construct AMatrix
cg=>operation: execute CG
out=>operation: output the resolt
st->inr->bg->sl->bl->int->A1->cg->out->e
###Reference
article{BarronPoole2016,
author = {Jonathan T Barron and Ben Poole},
title = {The Fast Bilateral Solver},
journal = {ECCV},
year = {2016},
}
@article{Barron2015A,
author = {Jonathan T Barron and Andrew Adams and YiChang Shih and Carlos Hern\'andez},
title = {Fast Bilateral-Space Stereo for Synthetic Defocus},
journal = {CVPR},
year = {2015},
}
@article{Adams2010,
author = {Andrew Adams Jongmin Baek Abe Davis},
title = {Fast High-Dimensional Filtering Using the Permutohedral Lattice},
journal = {Eurographics},
year = {2010},
}
##Installation Instructions
This is just a suggestion on how to build OpenCV 3.3. There a plenty of options. Also some packages might be optional.
sudo apt-get install libgtk2.0-dev pkg-config libavcodec-dev libavformat-dev libswscale-dev python-dev python-numpy libtbb2 libtbb-dev libjpeg-dev libpng-dev libtiff-dev libjasper-dev libdc1394-22-dev
git clone https://github.com/opencv/opencv.git
git clone https://github.com/opencv/opencv_contrib.git
cd opencv
mkdir build
cd build
cmake -D CMAKE_BUILD_TYPE=RELEASE -D CMAKE_INSTALL_PREFIX=/usr/local -D WITH_TBB=ON -D BUILD_NEW_PYTHON_SUPPORT=ON -D WITH_V4L=ON -D INSTALL_C_EXAMPLES=ON -D INSTALL_PYTHON_EXAMPLES=ON -D BUILD_EXAMPLES=ON -D WITH_QT=ON -D WITH_OPENGL=ON -D BUILD_TIFF=ON -DBUILD_opencv_viz=OFF -DWITH_VTK=OFF WITH_EIGEN=ON -D BUILD_EXAMPLES=ON -DOPENCV_EXTRA_MODULES_PATH=<opencv_contrib>/modules ..
make -j
sudo make install
Remember change **opencv_contrib ** to your own opencv_contrib path. This will create two demos that include in OpenCV executable examples, that you can run as shown in below.
- You can also play this colorization demo on your own device if you build opencv with the flag -DBUILD_EXAMPLES=ON by command like this:
#in you opencv build folder
./bin/example_ximgproc_colorize YOUR/OWN/PICTURE --dst_path=PATH/YOU/WANT/TO/SAVE/RESULT
- Some results from this moudle:
- the target for superresolution and the result of the bilateral solver is below:
the target.
the result of fast bilateral solver. - The dataset is so big that I didn't add this demo to the opencv_contrib. You can also try a stereo example that use the bilateral solver by execute the opencv/build/bin/example_ximgproc_disparity_filtering, and remember set the flag --filter=fbs_conf.
##Basic Usage
cv::ximgproc::fastBilateralSolverFilter(reference,target,confidence,result,
spatialSigma,lumaSigma,chromaSigma,100);
Firstly, we use the reference image mat_R construct a BilateralGrid, the we launch a depthsuperresolution to optimize the target image mat_T. The parameter spatialSigma is the Gaussian kernal for coordinate x y, similarly , the lumaSigma correspond luma(Y) and the chromaSigma correspond chroma(UV). It need to be noted that he mat_R should be covert to YUV form before construct the bilateralgrid.
###Colorization
cv::cvtColor(target, target, cv::COLOR_BGR2YCrCb);
std::vector<cv::Mat> src_channels;
std::vector<cv::Mat> dst_channels;
cv::split(target,src_channels);
cv::Mat result1 = cv::Mat(mat_input_gray.size(),mat_input_gray.type());
cv::Mat result2 = cv::Mat(mat_input_gray.size(),mat_input_gray.type());
filtering_time = (double)getTickCount();
dst_channels.push_back(src_channels[0]);
cv::ximgproc::fastBilateralSolverFilter(src_channels[0],src_channels[1],mat_input_confidence,
result1,sigma_spatial,sigma_luma,sigma_chroma);
dst_channels.push_back(result1);
cv::ximgproc::fastBilateralSolverFilter(src_channels[0],src_channels[2],mat_input_confidence,
result2,sigma_spatial,sigma_luma,sigma_chroma);
dst_channels.push_back(result2);
cv::merge(dst_channels,target);
cv::cvtColor(target, target, cv::COLOR_YCrCb2BGR);
Similar to above, we need to covert the imput image mat_in(gray image for colorization) to YUV form, then draw the gray image. when the drawing finished, press "ESC" twice to launch the colorization procession. the result will be save in specified folder. ###FastBilaterSolverFilter
Ptr< FastBilateralSolverFilter> fbs = createFastBilateralSolverFilter(guide,
sigma_spatial, sigma_luma, sigma_chroma, num_iter, max_tol);
fbs->filter(src, confidence, dst);
Similar to BilateralGrid, the PermutohedralLattce also need spatial parameter and the color parameter to specified the Gaussian kernel.
##Schedule
| Item | State | Remark |
|---|---|---|
| C++ code of the core algorithm | Completed | also python |
| Depthsuperres module | Completed | optimized |
| Colorization module | Completed | now in opencv example |
| PermutohedralLatticeFilter | Completed | will not contribe to opencv |
| Contribute project to OpenCV | Completed | with sample and test file |
| Detail Documentation | Completed | this toturial |