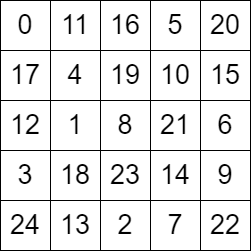
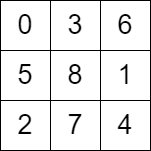
There is a knight on an n x n chessboard. In a valid configuration, the knight starts at the top-left cell of the board and visits every cell on the board exactly once.
You are given an n x n integer matrix grid consisting of distinct integers from the range [0, n * n - 1] where grid[row][col] indicates that the cell (row, col) is the grid[row][col]th cell that the knight visited. The moves are 0-indexed.
Return true if grid represents a valid configuration of the knight's movements or false otherwise.
Note that a valid knight move consists of moving two squares vertically and one square horizontally, or two squares horizontally and one square vertically. The figure below illustrates all the possible eight moves of a knight from some cell.
Input: grid = [[0,11,16,5,20],[17,4,19,10,15],[12,1,8,21,6],[3,18,23,14,9],[24,13,2,7,22]] Output: true Explanation: The above diagram represents the grid. It can be shown that it is a valid configuration.
Input: grid = [[0,3,6],[5,8,1],[2,7,4]] Output: false Explanation: The above diagram represents the grid. The 8th move of the knight is not valid considering its position after the 7th move.
n == grid.length == grid[i].length3 <= n <= 70 <= grid[row][col] < n * n- All integers in
gridare unique.
impl Solution {
pub fn check_valid_grid(grid: Vec<Vec<i32>>) -> bool {
let mut movements = vec![(0, 0); grid.len().pow(2)];
for row in 0..grid.len() {
for col in 0..grid.len() {
movements[grid[row][col] as usize] = (row as i32, col as i32);
}
}
if movements[0] != (0, 0) {
return false;
}
for i in 1..movements.len() {
let x = (movements[i].0 - movements[i - 1].0).abs();
let y = (movements[i].1 - movements[i - 1].1).abs();
if x * y != 2 {
return false;
}
}
true
}
}