Skip to content

Latest commit

 

History

History
77 lines (63 loc) · 2.54 KB

README.md

File metadata and controls

77 lines (63 loc) · 2.54 KB
Raw

2415. Reverse Odd Levels of Binary Tree

Given the root of a perfect binary tree, reverse the node values at each odd level of the tree.

  • For example, suppose the node values at level 3 are [2,1,3,4,7,11,29,18], then it should become [18,29,11,7,4,3,1,2].

Return the root of the reversed tree.

A binary tree is perfect if all parent nodes have two children and all leaves are on the same level.

The level of a node is the number of edges along the path between it and the root node.

Example 1:

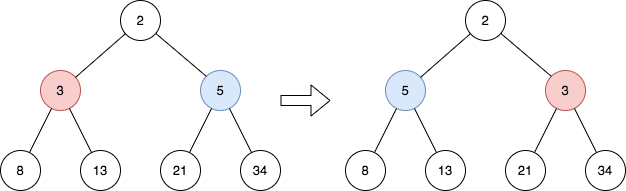
Input: root = [2,3,5,8,13,21,34]
Output: [2,5,3,8,13,21,34]
Explanation:
The tree has only one odd level.
The nodes at level 1 are 3, 5 respectively, which are reversed and become 5, 3.

Example 2:

Input: root = [7,13,11]
Output: [7,11,13]
Explanation:
The nodes at level 1 are 13, 11, which are reversed and become 11, 13.

Example 3:

Input: root = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]
Output: [0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]
Explanation:
The odd levels have non-zero values.
The nodes at level 1 were 1, 2, and are 2, 1 after the reversal.
The nodes at level 3 were 1, 1, 1, 1, 2, 2, 2, 2, and are 2, 2, 2, 2, 1, 1, 1, 1 after the reversal.

Constraints:

  • The number of nodes in the tree is in the range [1, 214].
  • 0 <= Node.val <= 105
  • root is a perfect binary tree.

Solutions (Python)

1. Solution

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def reverseOddLevels(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        isOdd = False
        currLevel = [root]

        while currLevel:
            nextLevel = []
            if currLevel[0].left is not None:
                for node in currLevel:
                    nextLevel.append(node.left)
                    nextLevel.append(node.right)

            isOdd = not isOdd
            currLevel = nextLevel

            if isOdd:
                currVals = [node.val for node in currLevel[::-1]]
                for i in range(len(currLevel)):
                    currLevel[i].val = currVals[i]

        return root