You are given a 2D integer array tiles where tiles[i] = [li, ri] represents that every tile j in the range li <= j <= ri is colored white.
You are also given an integer carpetLen, the length of a single carpet that can be placed anywhere.
Return the maximum number of white tiles that can be covered by the carpet.
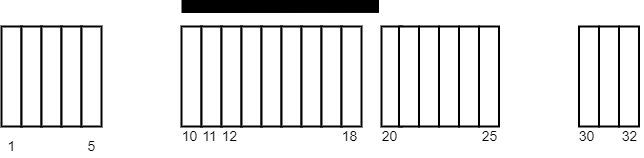
Input: tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 10 Output: 9 Explanation: Place the carpet starting on tile 10. It covers 9 white tiles, so we return 9. Note that there may be other places where the carpet covers 9 white tiles. It can be shown that the carpet cannot cover more than 9 white tiles.
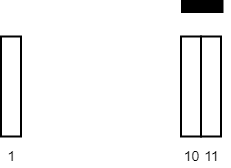
Input: tiles = [[10,11],[1,1]], carpetLen = 2 Output: 2 Explanation: Place the carpet starting on tile 10. It covers 2 white tiles, so we return 2.
1 <= tiles.length <= 5 * 104tiles[i].length == 21 <= li <= ri <= 1091 <= carpetLen <= 109- The
tilesare non-overlapping.
impl Solution {
pub fn maximum_white_tiles(tiles: Vec<Vec<i32>>, carpet_len: i32) -> i32 {
let mut tiles = tiles;
let mut prefix_sum = vec![0; tiles.len() + 1];
let mut ret = 0;
tiles.sort_unstable();
for i in 1..prefix_sum.len() {
prefix_sum[i] = prefix_sum[i - 1] + tiles[i - 1][1] - tiles[i - 1][0] + 1;
}
for i in 0..tiles.len() {
let j = tiles
.binary_search(&vec![tiles[i][0] + carpet_len, i32::MAX])
.unwrap_err();
if tiles[j - 1][1] < tiles[i][0] + carpet_len {
ret = ret.max(prefix_sum[j] - prefix_sum[i]);
} else {
ret = ret.max(
prefix_sum[j] - prefix_sum[i] - tiles[j - 1][1] - tiles[i][0] - carpet_len,
);
}
let j = tiles
.binary_search(&vec![tiles[i][1] - carpet_len, i32::MAX])
.unwrap_err();
if j == 0 || tiles[j - 1][1] <= tiles[i][1] - carpet_len {
ret = ret.max(prefix_sum[i + 1] - prefix_sum[j]);
} else {
ret = ret.max(
prefix_sum[i + 1] - prefix_sum[j] + tiles[j - 1][1] - tiles[i][1] + carpet_len,
);
}
}
ret
}
}