README.md

2192. All Ancestors of a Node in a Directed Acyclic Graph

You are given a positive integer n representing the number of nodes of a Directed Acyclic Graph (DAG). The nodes are numbered from 0 to n - 1 (inclusive).

You are also given a 2D integer array edges, where edges[i] = [fromi, toi] denotes that there is a unidirectional edge from fromi to toi in the graph.

Return a list answer, where answer[i] is the list of ancestors of the ith node, sorted in ascending order.

A node u is an ancestor of another node v if u can reach v via a set of edges.

Example 1:

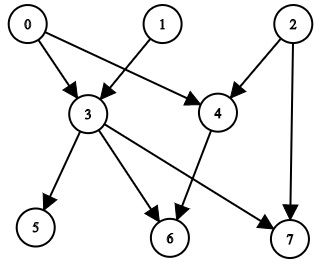
Input: n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
Output: [[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.
- Nodes 0, 1, and 2 do not have any ancestors.
- Node 3 has two ancestors 0 and 1.
- Node 4 has two ancestors 0 and 2.
- Node 5 has three ancestors 0, 1, and 3.
- Node 6 has five ancestors 0, 1, 2, 3, and 4.
- Node 7 has four ancestors 0, 1, 2, and 3.

Example 2:

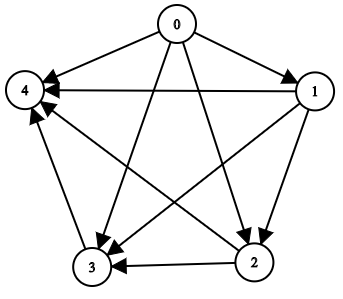
Input: n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
Output: [[],[0],[0,1],[0,1,2],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.
- Node 0 does not have any ancestor.
- Node 1 has one ancestor 0.
- Node 2 has two ancestors 0 and 1.
- Node 3 has three ancestors 0, 1, and 2.
- Node 4 has four ancestors 0, 1, 2, and 3.

Constraints:

• 1 <= n <= 1000
• 0 <= edges.length <= min(2000, n * (n - 1) / 2)
• edges[i].length == 2
• 0 <= fromi, toi <= n - 1
• fromi != toi
• There are no duplicate edges.
• The graph is directed and acyclic.

Solutions (Python)

1. Solution

class Solution:
    def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:
        indegrees = [0] * n
        ancestors = [set() for _ in range(n)]
        children = [[] for _ in range(n)]
        nodes = []
        answer = [[] for _ in range(n)]

        for u, v in edges:
            indegrees[v] += 1
            children[u].append(v)

        for i in range(n):
            if indegrees[i] == 0:
                nodes.append(i)

        while nodes != []:
            i = nodes.pop()
            answer[i] = sorted(ancestors[i])

            for j in children[i]:
                indegrees[j] -= 1
                ancestors[j].add(i)
                ancestors[j] |= ancestors[i]
                if indegrees[j] == 0:
                    nodes.append(j)

        return answer