You are given a stream of points on the X-Y plane. Design an algorithm that:
- Adds new points from the stream into a data structure. Duplicate points are allowed and should be treated as different points.
- Given a query point, counts the number of ways to choose three points from the data structure such that the three points and the query point form an axis-aligned square with positive area.
An axis-aligned square is a square whose edges are all the same length and are either parallel or perpendicular to the x-axis and y-axis.
Implement the DetectSquares class:
DetectSquares()Initializes the object with an empty data structure.void add(int[] point)Adds a new pointpoint = [x, y]to the data structure.int count(int[] point)Counts the number of ways to form axis-aligned squares with pointpoint = [x, y]as described above.
Input:
["DetectSquares", "add", "add", "add", "count", "count", "add", "count"]
[[], [[3, 10]], [[11, 2]], [[3, 2]], [[11, 10]], [[14, 8]], [[11, 2]], [[11, 10]]]
Output:
[null, null, null, null, 1, 0, null, 2]
Explanation:
DetectSquares detectSquares = new DetectSquares();
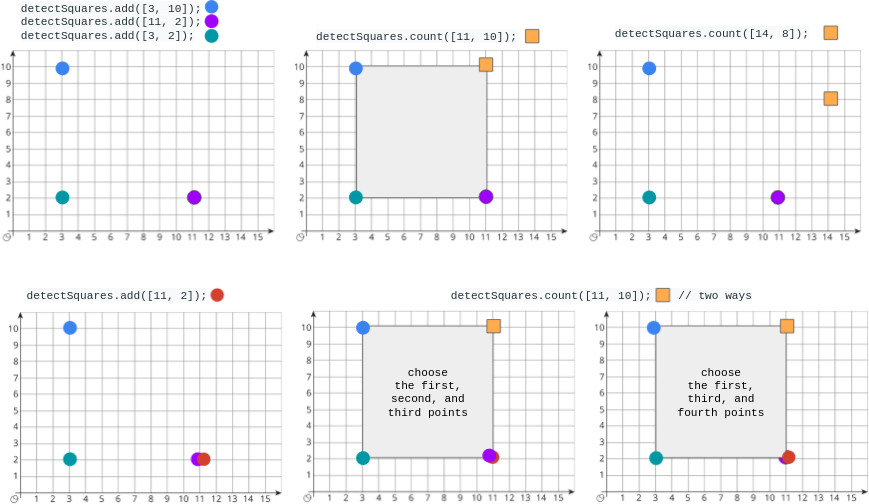
detectSquares.add([3, 10]);
detectSquares.add([11, 2]);
detectSquares.add([3, 2]);
detectSquares.count([11, 10]); // return 1. You can choose:
// - The first, second, and third points
detectSquares.count([14, 8]); // return 0. The query point cannot form a square with any points in the data structure.
detectSquares.add([11, 2]); // Adding duplicate points is allowed.
detectSquares.count([11, 10]); // return 2. You can choose:
// - The first, second, and third points
// - The first, third, and fourth points
point.length == 20 <= x, y <= 1000- At most
3000calls in total will be made toaddandcount.
use std::collections::HashMap;
struct DetectSquares {
points: HashMap<(i32, i32), i32>,
diagonals: HashMap<(i32, i32), Vec<(i32, i32)>>,
}
/**
* `&self` means the method takes an immutable reference.
* If you need a mutable reference, change it to `&mut self` instead.
*/
impl DetectSquares {
fn new() -> Self {
Self {
points: HashMap::new(),
diagonals: HashMap::new(),
}
}
fn add(&mut self, point: Vec<i32>) {
let (x, y) = (point[0], point[1]);
*self.points.entry((x, y)).or_insert(0) += 1;
self.diagonals
.entry((1, y - x))
.or_insert(vec![])
.push((x, y));
self.diagonals
.entry((-1, y + x))
.or_insert(vec![])
.push((x, y));
}
fn count(&self, point: Vec<i32>) -> i32 {
let (x0, y0) = (point[0], point[1]);
let mut ret = 0;
for &(x1, y1) in self.diagonals.get(&(1, y0 - x0)).unwrap_or(&vec![]) {
if x1 == x0 {
continue;
}
let count0 = *self.points.get(&(x0, y1)).unwrap_or(&0);
let count1 = *self.points.get(&(x1, y0)).unwrap_or(&0);
ret += count0 * count1;
}
for &(x1, y1) in self.diagonals.get(&(-1, y0 + x0)).unwrap_or(&vec![]) {
if x1 == x0 {
continue;
}
let count0 = *self.points.get(&(x0, y1)).unwrap_or(&0);
let count1 = *self.points.get(&(x1, y0)).unwrap_or(&0);
ret += count0 * count1;
}
ret
}
}
/**
* Your DetectSquares object will be instantiated and called as such:
* let obj = DetectSquares::new();
* obj.add(point);
* let ret_2: i32 = obj.count(point);
*/