Skip to content

Latest commit

 

History

History
101 lines (85 loc) · 4.16 KB

README_CN.md

File metadata and controls

101 lines (85 loc) · 4.16 KB
Raw

1606. 找到处理最多请求的服务器

你有 k 个服务器，编号为 0 到 k-1 ，它们可以同时处理多个请求组。每个服务器有无穷的计算能力但是 不能同时处理超过一个请求 。请求分配到服务器的规则如下：

  • 第 i （序号从 0 开始）个请求到达。
  • 如果所有服务器都已被占据，那么该请求被舍弃（完全不处理）。
  • 如果第 (i % k) 个服务器空闲，那么对应服务器会处理该请求。
  • 否则，将请求安排给下一个空闲的服务器（服务器构成一个环，必要的话可能从第 0 个服务器开始继续找下一个空闲的服务器）。比方说，如果第 i 个服务器在忙，那么会查看第 (i+1) 个服务器，第 (i+2) 个服务器等等。

给你一个 严格递增 的正整数数组 arrival ，表示第 i 个任务的到达时间，和另一个数组 load ，其中 load[i] 表示第 i 个请求的工作量（也就是服务器完成它所需要的时间）。你的任务是找到 最繁忙的服务器 。最繁忙定义为一个服务器处理的请求数是所有服务器里最多的。

请你返回包含所有 最繁忙服务器 序号的列表，你可以以任意顺序返回这个列表。

示例 1:

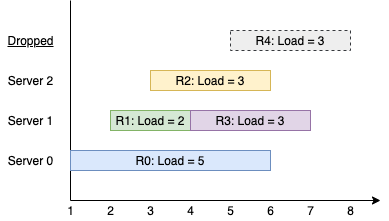
输入: k = 3, arrival = [1,2,3,4,5], load = [5,2,3,3,3]
输出: [1]
解释:
所有服务器一开始都是空闲的。
前 3 个请求分别由前 3 台服务器依次处理。
请求 3 进来的时候，服务器 0 被占据，所以它被安排到下一台空闲的服务器，也就是服务器 1 。
请求 4 进来的时候，由于所有服务器都被占据，该请求被舍弃。
服务器 0 和 2 分别都处理了一个请求，服务器 1 处理了两个请求。所以服务器 1 是最忙的服务器。

示例 2:

输入: k = 3, arrival = [1,2,3,4], load = [1,2,1,2]
输出: [0]
解释:
前 3 个请求分别被前 3 个服务器处理。
请求 3 进来，由于服务器 0 空闲，它被服务器 0 处理。
服务器 0 处理了两个请求，服务器 1 和 2 分别处理了一个请求。所以服务器 0 是最忙的服务器。

示例 3:

输入: k = 3, arrival = [1,2,3], load = [10,12,11]
输出: [0,1,2]
解释: 每个服务器分别处理了一个请求，所以它们都是最忙的服务器。

示例 4:

输入: k = 3, arrival = [1,2,3,4,8,9,10], load = [5,2,10,3,1,2,2]
输出: [1]

示例 5:

输入: k = 1, arrival = [1], load = [1]
输出: [0]

提示:

  • 1 <= k <= 105
  • 1 <= arrival.length, load.length <= 105
  • arrival.length == load.length
  • 1 <= arrival[i], load[i] <= 109
  • arrival 保证 严格递增 。

题解 (Rust)

1. 题解

use std::cmp::Reverse;
use std::collections::BinaryHeap;

impl Solution {
    pub fn busiest_servers(k: i32, arrival: Vec<i32>, load: Vec<i32>) -> Vec<i32> {
        let k = k as usize;
        let mut free = (0..k).map(|i| Reverse(i)).collect::<BinaryHeap<_>>();
        let mut busy = BinaryHeap::new();
        let mut count = vec![0; load.len()];

        for i in 0..load.len() {
            while let Some(&(Reverse(t), j)) = busy.peek() {
                if t > arrival[i] {
                    break;
                } else if i % k > j {
                    free.push(Reverse(j + i / k * k + k));
                } else {
                    free.push(Reverse(j + i / k * k));
                }
                busy.pop();
            }

            if let Some(Reverse(j)) = free.pop() {
                busy.push((Reverse(arrival[i] + load[i]), j % k));
                count[j % k] += 1;
            }
        }

        let max_count = *count.iter().max().unwrap();

        (0..k as i32)
            .filter(|&i| *count.get(i as usize).unwrap_or(&0) == max_count)
            .collect()
    }
}