Given an m x n binary matrix mat, return the number of submatrices that have all ones.
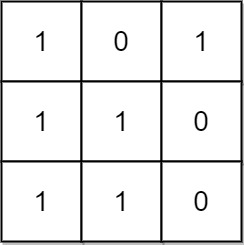
Input: mat = [[1,0,1],[1,1,0],[1,1,0]] Output: 13 Explanation: There are 6 rectangles of side 1x1. There are 2 rectangles of side 1x2. There are 3 rectangles of side 2x1. There is 1 rectangle of side 2x2. There is 1 rectangle of side 3x1. Total number of rectangles = 6 + 2 + 3 + 1 + 1 = 13.
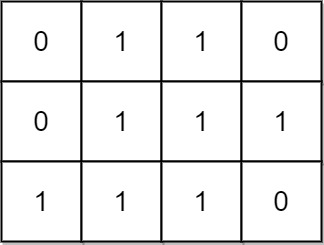
Input: mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]] Output: 24 Explanation: There are 8 rectangles of side 1x1. There are 5 rectangles of side 1x2. There are 2 rectangles of side 1x3. There are 4 rectangles of side 2x1. There are 2 rectangles of side 2x2. There are 2 rectangles of side 3x1. There is 1 rectangle of side 3x2. Total number of rectangles = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24.
1 <= m, n <= 150mat[i][j]is either0or1.
impl Solution {
pub fn num_submat(mat: Vec<Vec<i32>>) -> i32 {
let m = mat.len();
let n = mat[0].len();
let mut mat = mat;
let mut ret = 0;
for i in 0..m {
for j in 0..n {
if mat[i][j] == 1 {
let mut min_count = i32::MAX;
if j > 0 {
mat[i][j] += mat[i][j - 1];
}
for k in (0..=i).rev() {
if mat[k][j] == 0 {
break;
}
min_count = min_count.min(mat[k][j]);
ret += min_count;
}
}
}
}
ret
}
}