README.md

1443. Minimum Time to Collect All Apples in a Tree

Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at vertex 0 and coming back to this vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [ai, bi] means that exists an edge connecting the vertices ai and bi. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple; otherwise, it does not have any apple.

Example 1:

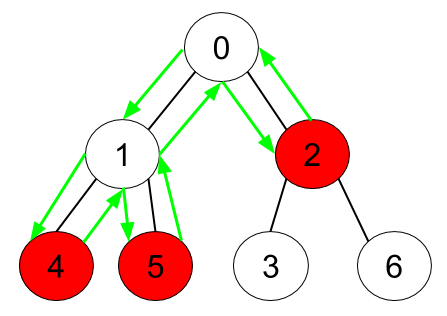
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.

Example 2:

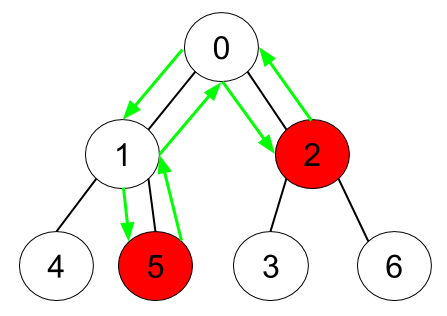
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.

Example 3:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
Output: 0

Constraints:

• 1 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai < bi <= n - 1
• hasApple.length == n

Solutions (Rust)

1. Solution

use std::collections::HashSet;

impl Solution {
    pub fn min_time(n: i32, edges: Vec<Vec<i32>>, mut has_apple: Vec<bool>) -> i32 {
        let n = n as usize;
        let mut children = vec![HashSet::new(); n];
        let mut parent = vec![n; n];
        let mut nodes = vec![0];

        for edge in &edges {
            children[edge[0] as usize].insert(edge[1] as usize);
            children[edge[1] as usize].insert(edge[0] as usize);
        }

        while let Some(node) = nodes.pop() {
            children[node].remove(&parent[node]);

            for &child in children[node].iter() {
                parent[child] = node;
                nodes.push(child);
            }
        }

        for node in 0..n {
            if children[node].is_empty() {
                nodes.push(node);
            }
        }

        while let Some(node) = nodes.pop() {
            if node == 0 {
                break;
            }

            has_apple[parent[node]] |= has_apple[node];
            children[parent[node]].remove(&node);
            if children[parent[node]].is_empty() {
                nodes.push(parent[node]);
            }
        }

        ((0..n).filter(|&node| has_apple[node]).count() as i32 - 1).max(0) * 2
    }
}