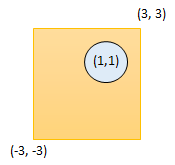README.md

1401. Circle and Rectangle Overlapping

Given a circle represented as (radius, x_center, y_center) and an axis-aligned rectangle represented as (x1, y1, x2, y2), where (x1, y1) are the coordinates of the bottom-left corner, and (x2, y2) are the coordinates of the top-right corner of the rectangle.

Return True if the circle and rectangle are overlapped otherwise return False.

In other words, check if there are any point (xi, yi) such that belongs to the circle and the rectangle at the same time.

Example 1:

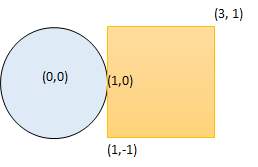
Input: radius = 1, x_center = 0, y_center = 0, x1 = 1, y1 = -1, x2 = 3, y2 = 1
Output: true
Explanation: Circle and rectangle share the point (1,0)

Example 2:

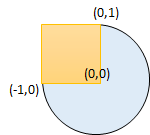
Input: radius = 1, x_center = 0, y_center = 0, x1 = -1, y1 = 0, x2 = 0, y2 = 1
Output: true

Example 3:

Input: radius = 1, x_center = 1, y_center = 1, x1 = -3, y1 = -3, x2 = 3, y2 = 3
Output: true

Example 4:

Input: radius = 1, x_center = 1, y_center = 1, x1 = 1, y1 = -3, x2 = 2, y2 = -1
Output: false

Constraints:

• 1 <= radius <= 2000
• -10^4 <= x_center, y_center, x1, y1, x2, y2 <= 10^4
• x1 < x2
• y1 < y2

Solutions (Rust)

1. Solution

impl Solution {
    pub fn check_overlap(radius: i32, x_center: i32, y_center: i32, x1: i32, y1: i32, x2: i32, y2: i32) -> bool {
        let x = if x_center >= x1 && x_center <= x2 {
            0
        } else {
            (x_center - x1).abs().min((x_center - x2).abs())
        };
        let y = if y_center >= y1 && y_center <= y2 {
            0
        } else {
            (y_center - y1).abs().min((y_center - y2).abs())
        };

        x * x + y * y <= radius * radius
    }
}