README.md

1391. Check if There is a Valid Path in a Grid

You are given an m x n grid. Each cell of grid represents a street. The street of grid[i][j] can be:

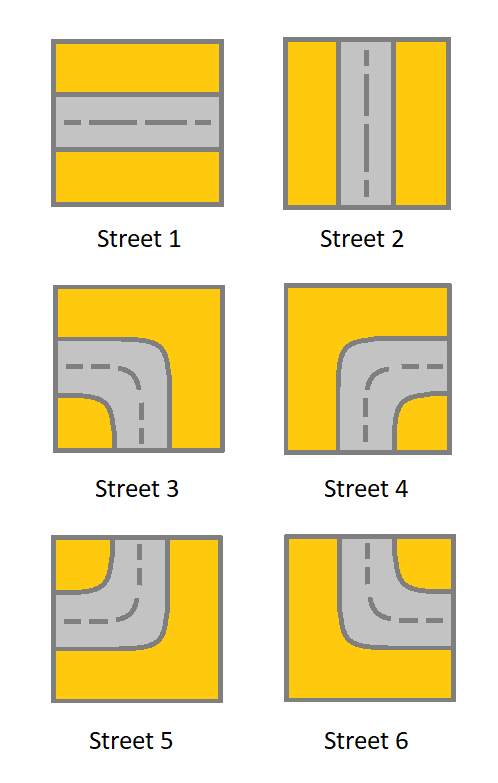
• 1 which means a street connecting the left cell and the right cell.
• 2 which means a street connecting the upper cell and the lower cell.
• 3 which means a street connecting the left cell and the lower cell.
• 4 which means a street connecting the right cell and the lower cell.
• 5 which means a street connecting the left cell and the upper cell.
• 6 which means a street connecting the right cell and the upper cell.

You will initially start at the street of the upper-left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1). The path should only follow the streets.

Notice that you are not allowed to change any street.

Return true if there is a valid path in the grid or false otherwise.

Example 1:

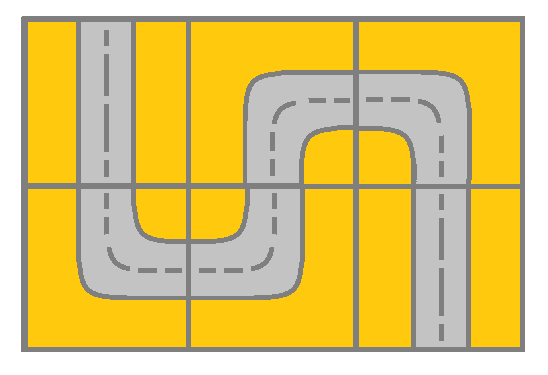
Input: grid = [[2,4,3],[6,5,2]]
Output: true
Explanation: As shown you can start at cell (0, 0) and visit all the cells of the grid to reach (m - 1, n - 1).

Example 2:

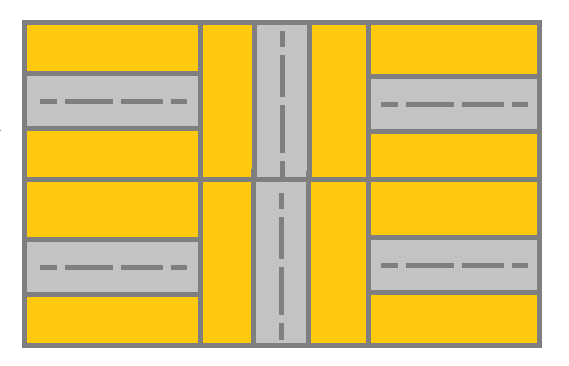
Input: grid = [[1,2,1],[1,2,1]]
Output: false
Explanation: As shown you the street at cell (0, 0) is not connected with any street of any other cell and you will get stuck at cell (0, 0)

Example 3:

Input: grid = [[1,1,2]]
Output: false
Explanation: You will get stuck at cell (0, 1) and you cannot reach cell (0, 2).

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• 1 <= grid[i][j] <= 6

Solutions (Rust)

1. Solution

use std::collections::HashSet;

impl Solution {
    pub fn has_valid_path(grid: Vec<Vec<i32>>) -> bool {
        let m = grid.len();
        let n = grid[0].len();
        let mut seen = HashSet::new();
        let mut cells = vec![(0, 0)];

        while let Some((i, j)) = cells.pop() {
            if i == m - 1 && j == n - 1 {
                return true;
            }

            seen.insert((i, j));

            match grid[i][j] {
                1 => {
                    if j > 0 && !seen.contains(&(i, j - 1)) && [1, 4, 6].contains(&grid[i][j - 1]) {
                        cells.push((i, j - 1));
                    }
                    if j + 1 < n
                        && !seen.contains(&(i, j + 1))
                        && [1, 3, 5].contains(&grid[i][j + 1])
                    {
                        cells.push((i, j + 1));
                    }
                }
                2 => {
                    if i > 0 && !seen.contains(&(i - 1, j)) && [2, 3, 4].contains(&grid[i - 1][j]) {
                        cells.push((i - 1, j));
                    }
                    if i + 1 < m
                        && !seen.contains(&(i + 1, j))
                        && [2, 5, 6].contains(&grid[i + 1][j])
                    {
                        cells.push((i + 1, j));
                    }
                }
                3 => {
                    if j > 0 && !seen.contains(&(i, j - 1)) && [1, 4, 6].contains(&grid[i][j - 1]) {
                        cells.push((i, j - 1));
                    }
                    if i + 1 < m
                        && !seen.contains(&(i + 1, j))
                        && [2, 5, 6].contains(&grid[i + 1][j])
                    {
                        cells.push((i + 1, j));
                    }
                }
                4 => {
                    if j + 1 < n
                        && !seen.contains(&(i, j + 1))
                        && [1, 3, 5].contains(&grid[i][j + 1])
                    {
                        cells.push((i, j + 1));
                    }
                    if i + 1 < m
                        && !seen.contains(&(i + 1, j))
                        && [2, 5, 6].contains(&grid[i + 1][j])
                    {
                        cells.push((i + 1, j));
                    }
                }
                5 => {
                    if i > 0 && !seen.contains(&(i - 1, j)) && [2, 3, 4].contains(&grid[i - 1][j]) {
                        cells.push((i - 1, j));
                    }
                    if j > 0 && !seen.contains(&(i, j - 1)) && [1, 4, 6].contains(&grid[i][j - 1]) {
                        cells.push((i, j - 1));
                    }
                }
                _ => {
                    if i > 0 && !seen.contains(&(i - 1, j)) && [2, 3, 4].contains(&grid[i - 1][j]) {
                        cells.push((i - 1, j));
                    }
                    if j + 1 < n
                        && !seen.contains(&(i, j + 1))
                        && [1, 3, 5].contains(&grid[i][j + 1])
                    {
                        cells.push((i, j + 1));
                    }
                }
            }
        }

        false
    }
}