README.md

935. Knight Dialer

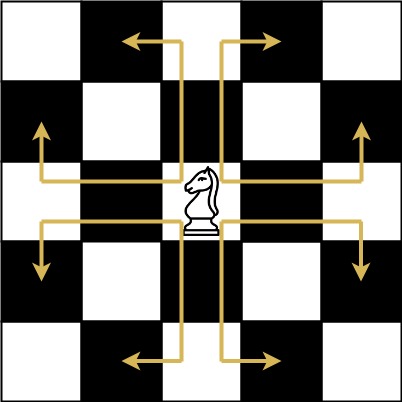
The chess knight has a unique movement, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L). The possible movements of chess knight are shown in this diagaram:

A chess knight can move as indicated in the chess diagram below:

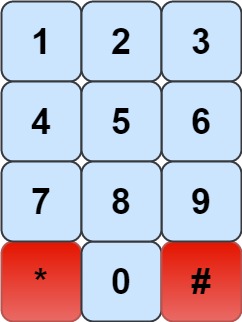
We have a chess knight and a phone pad as shown below, the knight can only stand on a numeric cell (i.e. blue cell).

Given an integer n, return how many distinct phone numbers of length n we can dial.

You are allowed to place the knight on any numeric cell initially and then you should perform n - 1 jumps to dial a number of length n. All jumps should be valid knight jumps.

As the answer may be very large, return the answer modulo 109 + 7.

Example 1:

Input: n = 1
Output: 10
Explanation: We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.

Example 2:

Input: n = 2
Output: 20
Explanation: All the valid number we can dial are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

Example 3:

Input: n = 3
Output: 46

Example 4:

Input: n = 4
Output: 104

Example 5:

Input: n = 3131
Output: 136006598
Explanation: Please take care of the mod.

Constraints:

• 1 <= n <= 5000

Solutions (Ruby)

1. Dynamic Programming

# @param {Integer} n
# @return {Integer}
def knight_dialer(n)
  dp = [1] * 10

  (1...n).each do |_|
    dp = [
      dp[4] + dp[6],
      dp[6] + dp[8],
      dp[7] + dp[9],
      dp[4] + dp[8],
      dp[0] + dp[3] + dp[9],
      0,
      dp[0] + dp[1] + dp[7],
      dp[2] + dp[6],
      dp[1] + dp[3],
      dp[2] + dp[4]
    ]
  end

  dp.sum % 1_000_000_007
end

Solutions (Rust)

1. Dynamic Programming

impl Solution {
    pub fn knight_dialer(n: i32) -> i32 {
        let mut dp = [1; 10];

        for _ in 1..n {
            let mut dp_ = [0; 10];
            for i in 0..10 {
                dp_[i] = match i {
                    0 => dp[4] + dp[6],
                    1 | 3 => dp[7 - i] + dp[8],
                    2 | 8 => dp[9 - i] + dp[11 - i],
                    4 | 6 => (dp[0] + dp[7 - i]) % 1_000_000_007 + dp[13 - i],
                    7 | 9 => dp[2] + dp[13 - i],
                    _ => 0,
                } % 1_000_000_007;
            }
            dp = dp_;
        }

        dp.iter().fold(0, |acc, x| (acc + x) % 1_000_000_007)
    }
}