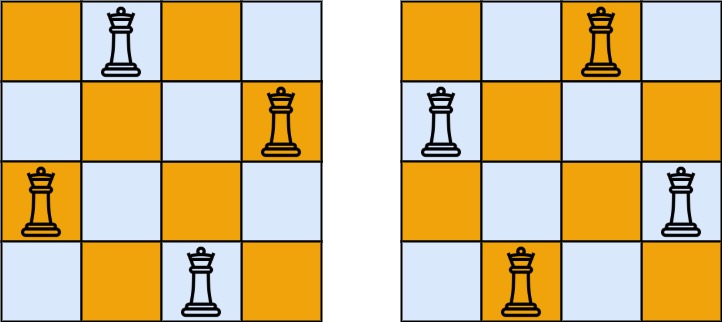
The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.
Input: n = 4 Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above
Input: n = 1 Output: [["Q"]]
1 <= n <= 9
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
ret = []
for ys in itertools.permutations(range(n)):
board = [['.'] * n for _ in range(n)]
for x, y in zip(range(n), ys):
if any(board[x - i][y - i] == 'Q' for i in range(1, min(x, y) + 1)) or \
any(board[x - i][y + i] == 'Q' for i in range(1, min(x, n - y - 1) + 1)):
break
board[x][y] = 'Q'
else:
ret.append([''.join(row) for row in board])
return ret