[Book 1, Chapter 9.1] Why reject vectors outside unit sphere? #1369
-
|
We generate vectors within unit cube and reject those that are outside of unit sphere. We then normalize them to be on the surface of the sphere. My question is: why do we reject vectors outside unit sphere? They can be normalized just like the other ones, and will end up on the surface of the sphere. What did I miss? |
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
Giving it a test, there isn't much of a difference (Left: But considering this is a sampling method, increasing the sampling threshold (in this case, to the whole unit cube) will caused there to be a disproportionate a mount of samples caught in the corners. Thus causing a slight skew. That's my understanding at least. @hollasch can tell me if I'm wrong or not :) |
Beta Was this translation helpful? Give feedback.

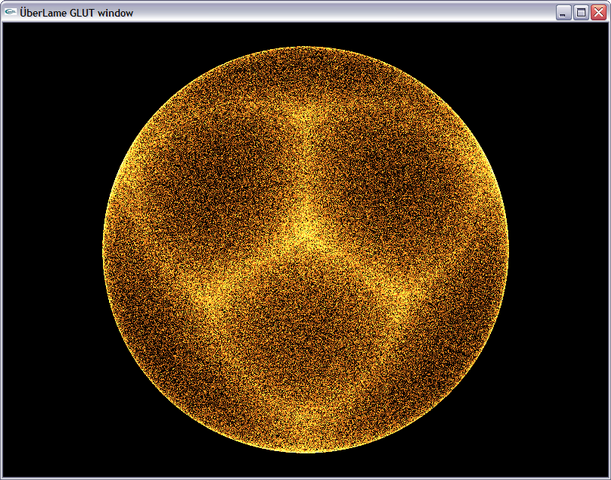
Yes, @rupsis is correct. All random points along the axes will lie inside the sphere. However, the cube diagonals will have not only that number of random points, but additional random points that were generated from the sphere to the unit corner — (√2)-1 more points, to be precise.
As a result, you get an image that looks like this:
See Generating random directions with uniform distribution
for a good article that covers this.